LLMs are secretly lossless text compressor and how to use it like one

Many people say that machine learning and data compression are two sides of the same coin. While this comparison is often debated, in this blog, I will connect Large Language Models (LLMs) with XZ (yes, that compression software), and how to enpower these compression software with LLMs to achieve much higher compression ratio losslessly, from the information theory perspective.

This blog post is largerly inspired by Shawn Tan’s blog and NNCP project

My own implementation is available here: https://github.com/zirui-ray-liu/text-compressor

Huffman Encoding with minimal bit length

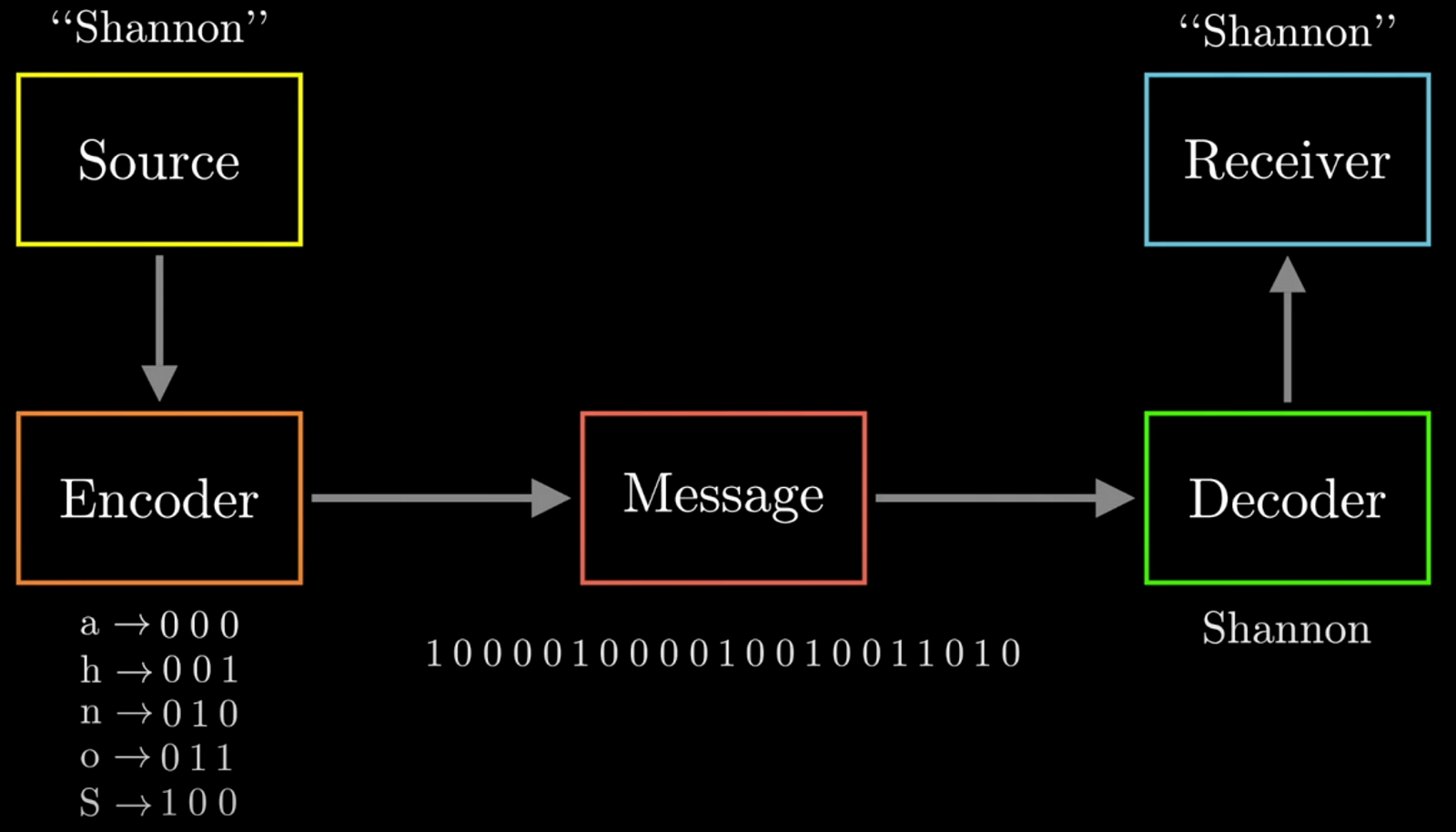
When you put English text into a computer, it saves every individual character as one btye of data. In the early days of computing, disk space for storing data was very limited. This led to a fundamental problem: What is the minimal bit length for storing a text file losslessly?

In information theory, finding the minimal description length means encoding data as efficiently as possible. In the above example, “Shannon” contains 5 unique characters (S, h, a, n, o), we can use 3 bits per character to distinguish each of them. With 7 characters in total, this encoding would require 7×3=21 bits. During decoding, we just greedy match the bit to characters from left to right. Can we do better?

Since the total bit length equals

One intuitive way to reduce the total bit length is to assign fewer bits to common characters and more bits to rarer ones, a concept known as variable-length encoding. For example, if “n” is the most frequent character in “Shannon,” we might assign it just 1 bit, while assigning other characters longer bit sequences. In this optimized encoding, we reduce the total bit length to 14 bits.  In practice, Huffman coding is an algorithm to help you find this optimal bit assignment automatically. It first count the frequency of all characters as input and assign the bit according to this frequency table. This technique forms the foundation of most modern compression tools, like XZ and Gzip, which use Huffman coding to reduce file sizes efficiently.

Why it is linked to LLMs?

Huffman coding assigns bit according to the frequency table of each possible character. In other words, it assigns bits according to the empirical distribution observed from the text file. Some implicit assumption behinds it are:

• The character distribution is a multinomial distribution with

• It treats different character locations equally with this multinomial distribution

We know that these assumptions are not hold in practice since language has structures. So how about we replace these character distribution with one given by a LLM? Let us analyze what will happen in this case:

LLMs are trained with the next word prediction, in other words, they are optimized for

where \(w_T\) are the next word to be predicted and \(w_1, \cdots, w_{T-1}\) are the previous workds. Let’s assume that the LLM is well-trained and can assign a high probability to the correct next word (much higher than a simple frequency-based probability derived from counting characters). In this scenario, Huffman coding becomes relevant. Recall that Huffman coding works by assigning fewer bits to more probable symbols, which means that more common characters (or words, in this case) get shorter codes. Therefore, if the LLM can assign a higher probability to the correct next word (compared to a basic character frequency count), it will effectively reduce the number of bits needed to represent that word, thanks to the principles of Huffman coding. From this perspective, LLMs are exactly trained to minimize description length for text files losslessly!

Implementation

Below is the psudo code of using LLMs for compressing text files.

\begin{algorithm}
\caption{Compression}
\begin{algorithmic}
\STATE Given a text sequence $w_1,\cdots,w_{T-1}$
\STATE Predict the $w_T$ distribution $P(w_T|w_1,\cdots, w_{T-1})$ with LLM 
\STATE Convert this distribution into pseudo frequency table by \texttt{Round}(10,000 * $P(w_T|w_1,\cdots, w_{T-1})$)
\STATE Construct the Huffman Tree with the frequency table and encode $w_T$ with the leaf bits
\STATE Repeat this process until all words are encoded
\end{algorithmic}
\end{algorithm}

\begin{algorithm}
\caption{Decompression}
\begin{algorithmic}
\STATE Given a bitstream and the text sequence $w_1,\cdots,w_{T-1}$ we have decompressed so far
\STATE Predict the $w_T$ distribution $P(w_T|w_1,\cdots, w_{T-1})$ with LLM 
\STATE Convert this distribution into pseudo frequency table by \texttt{Round}(10,000 * $P(w_T|w_1,\cdots, w_{T-1})$)
\STATE Construct the Huffman Tree with the frequency table
\STATE Walk the Huffman tree and match the next available bits in the bitstream.
\STATE Once we hit a leaf, decode the word $w_T$ and add it to the text sequence
\STATE Repeat this process until all bits in the bitstream are matched
\end{algorithmic}
\end{algorithm}

I implement the above algorithms, which is modified from the source code of NNCP project. The code is available here: https://github.com/zirui-ray-liu/text-compressor

This project is implemented in pure Python, leveraging the Huggingface Transformer API. We provide an example showcasing how GPT-2 can be used to compress a small text corpus from Wikipedia.

To compress the text, run the following command:

bash scripts/eval.sh

For the example text file unittest.txt (size: 4KB),the script should generate a compressed file unittest.bin (size: 542 Bytes) and a decompressed file decmp_unittest.txt.

For reference, using XZ with the command xz -9 unittest.txt produces a file unittest.txt.xz (size: 1.9KB), which is 3.5X larger than GPT2 based version.

Notes

• You can greatly improve the compression ratio with stronger LLMs

• You can use this framework to losslessly compress anything that can be formulated as next-something prediction