Rounding Errors of FP16 and its impact in Machine Learning

FP16 and BF16 are two most commonly used numerical precision in Machine Learning. In this blog we will discuss some abnormal behaviors of them.

Quick example (with torch 2.6.0):

>>>import torch
>>>a = torch.tensor(8.125, dtype=torch.float16)
>>>b = torch.tensor(1032, dtype=torch.float16)
>>>a + 1024 == b
tensor(True)

Why this happens

To understand this abnormal behavior, you first need to understand how computer encodes floating point numbers.

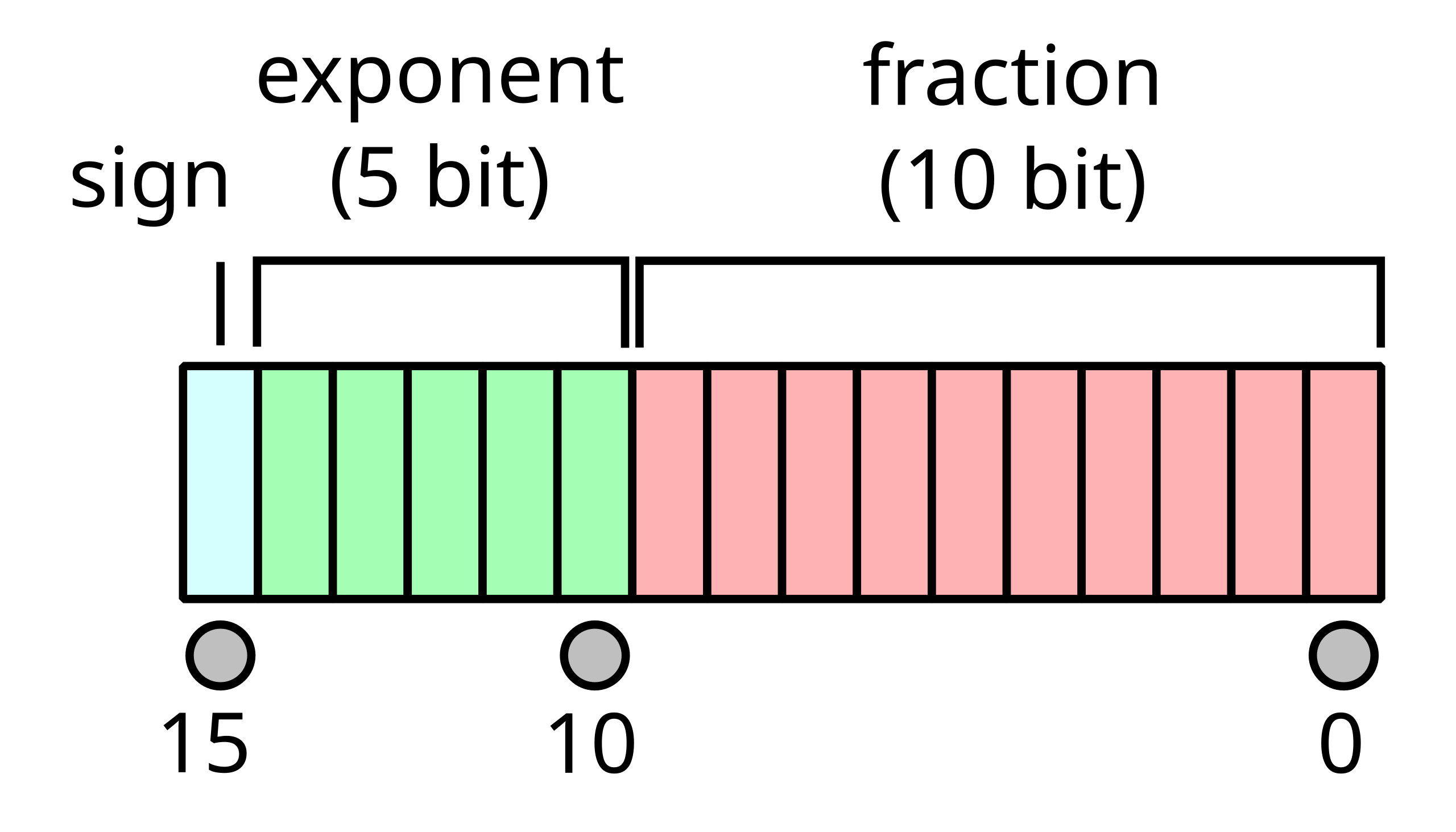
So in FP16, it has 1 sign bit, 5 exponent bits, and 10 mantissa bits. Every number can be expressed as

where S, E, and M are the decimal of the sign, exponent, and mantissa, respectively. For example,

The binary code of 8.125 in FP16 is 0100100000010000. In this case, S = 0, E = 18 (10010), M = 16 (0000010000), so

Now let’s examine what happens to 8.125 + 1024.

let b = 8.125 + 1024.

We know that the sign part S of b is 0. The exponent part E of b must be 25, since 25 - 15 == 10 (otherwise you cannot represent a number > 1024 && < 2048).

Now let’s examine the expression of b.

So if we write b in FP16, b is an integer! The original \(.125\) of \(8.125\) is rounded off in this case, which explain the beginning example.

For BF16, it assigns 8bits to exponent and 7bits to mantissa. So it does not the above failure patterns, however,it sacrifices the precision of fraction part.

Impacts to model training

This can get really bad when you perform model training since we update the gradient every step. In the worst case, this can leads to uncovergence (imagine every step you round off a small portion of weight parameters).

Thus, it is crusial to use a higher precision accumulator, which is the common practice in mixed precision training, i.e., we maintain a FP32 copy of model weights and optimizer states.