Implementing Flash-Attention with Softmax Offset (Sinks)

GPT-OSS have released and one notable feature is that each attention head now includes a learned bias term in the denominator of the softmax. This is similar to techniques like off-by-one attention and attention sinks.

Mathmatically, this is equvelent to

This Bias is a learnable positive variable assigned to each attention head. Intuitively, it provides the model with the option to ‘attend to nothing. To facilitate fast training and inference with this Softmax mechanism, we need to integrate it into Flash-Attention OP.

For the ease of understanding and implementation, in this blog I will modify the official triton FA2 tutorial to add this function. My own implementation is available here: https://github.com/zirui-ray-liu/FA2-with-Attn-Offset-Triton

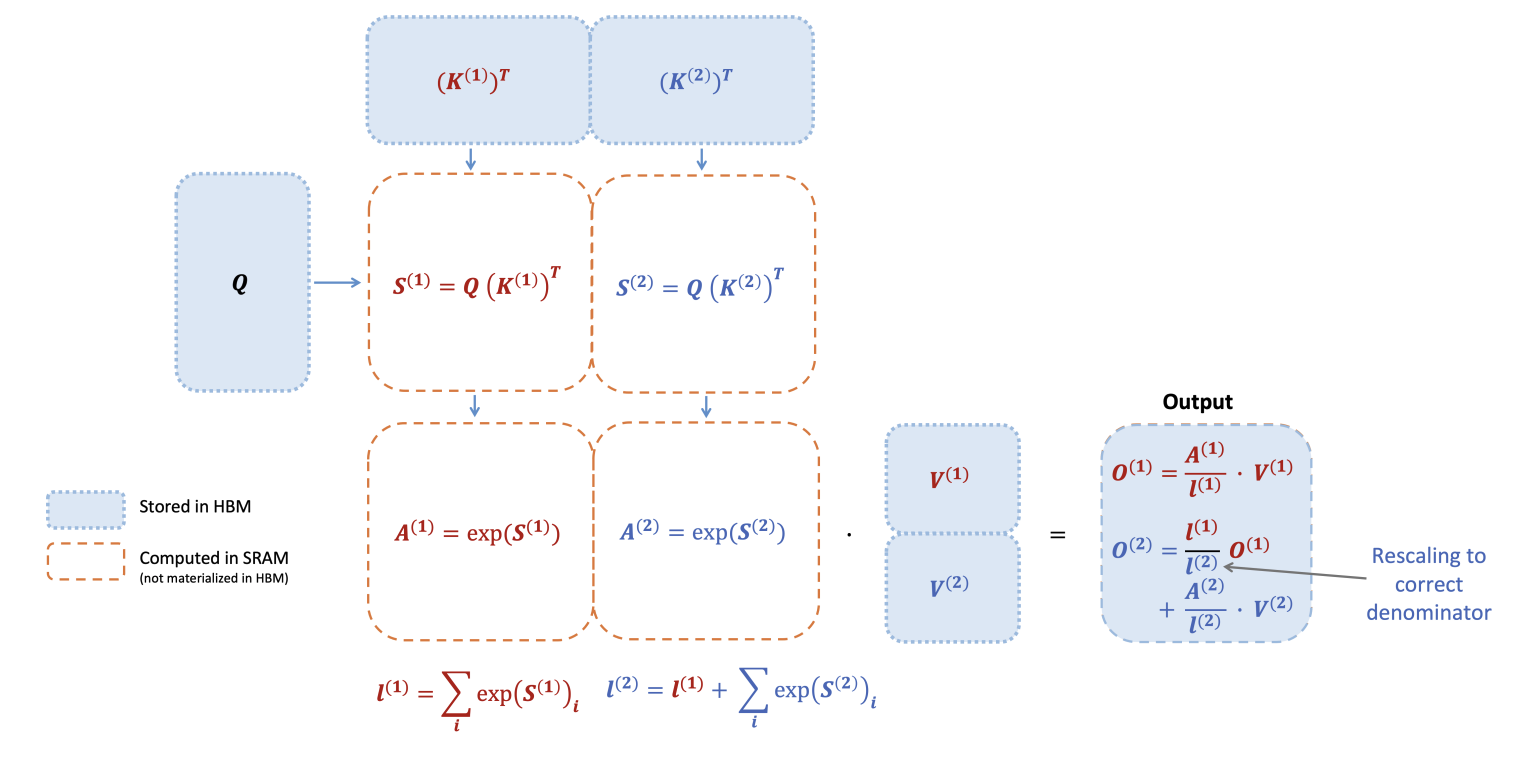
Flash-Attention-2 Forward Pass:

Flash-Attention-2 Backward Pass:

In the forward pass, the attention softmax is implemented with base-2 exponentials (In the triton implementation, it uses base-2 exponentials instead of base-e since base-2 is much more hardware friendly via bit-shifting): \(l_i = \sum_j 2^{s_{ij} - m_i}\) and at the epilogue: \(l_i \leftarrow l_i + \text{bias} \cdot 2^{-m_i}\)

Stored log-sum-exp (LSE): \(L_i = m_i + \log_2(l_i) = \log_2\!\big(\sum_j e^{s_{ij}} + \text{bias}\big)\)

Output: \(o_i = \frac{\sum_j 2^{s_{ij} - m_i} v_j}{l_i}\)

Define: \(\Delta_i = \langle o_i, do_i \rangle = \sum_k o_{ik}\, do_{ik}\)

In the original FA2 backward, $\Delta_i$ will be explicitly calculated before obtaining \(dQ, dK, dV\).

Since the bias appears only in the denominator, the gradient w.r.t. bias is: \(\frac{\partial \mathcal{L}}{\partial \text{bias}} = -\sum_i \frac{\Delta_i}{\sum_j e^{s_{ij}} + \text{bias}} = -\sum_i \Delta_i 2^{-M_i}.\)

Note this is implementation is not the most hardware-efficient one. But it is easy to understand and can be implemented with minimal line of changes.